Geometry 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflect over x= 1 reflection over the line y=x Reflection over y=x reflection over yaxis reflection where y=xAny line can be graphed using two points Select two x x values, and plug them into the equation to find the corresponding y y values Tap for more steps x y 0 −2 2 0 x y 0 2 2 0 A trend line will not work because it must be x=y Here is a link to the file in my dropbox if it helps anyone to look at it Register To Reply , 0624 PM #2 shg View Profile View Forum Posts Forum Guru Join Date Location The Great State of Texas MSOff Ver 03, 10 Posts
Solution How To Draw The Line Y X On Graph
Y=x line graph
Y=x line graph-Answer to Calculate the area of the segment cut from the curve y=x(3x) by the line y=x Also, sketch the graph By signing up, you'll getReflection over the line $$ y = x $$ A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the $$ y = x $$ $ (A,B) \rightarrow (\red B, \red A ) $ Diagram 6 Applet You can drag the point anywhere you want
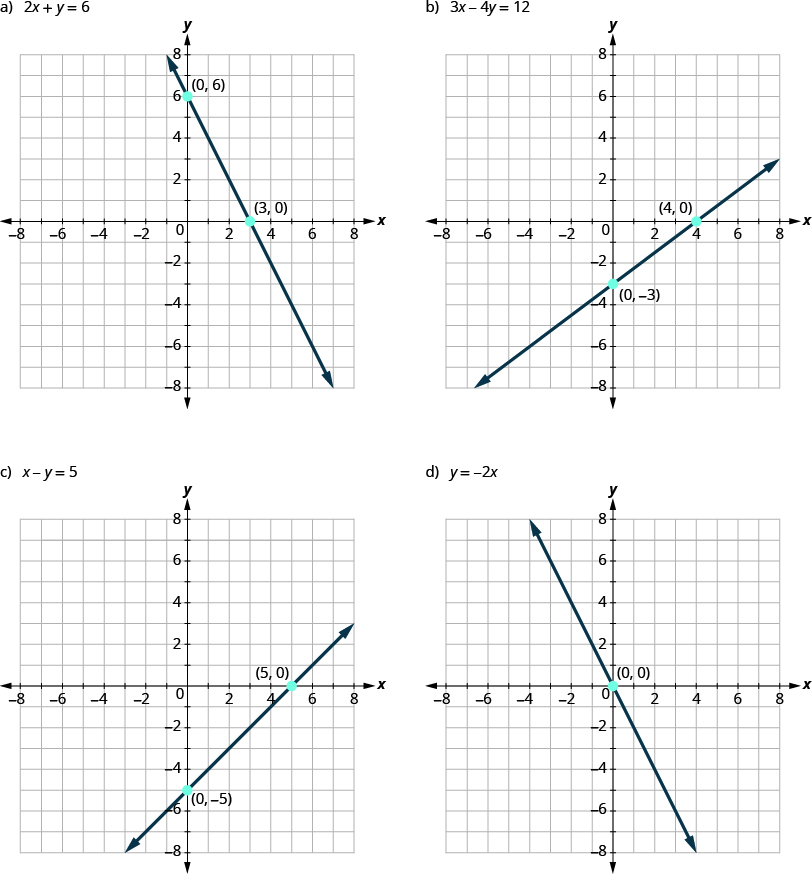



Identifying The Intercepts On The Graph Of A Line Prealgebra
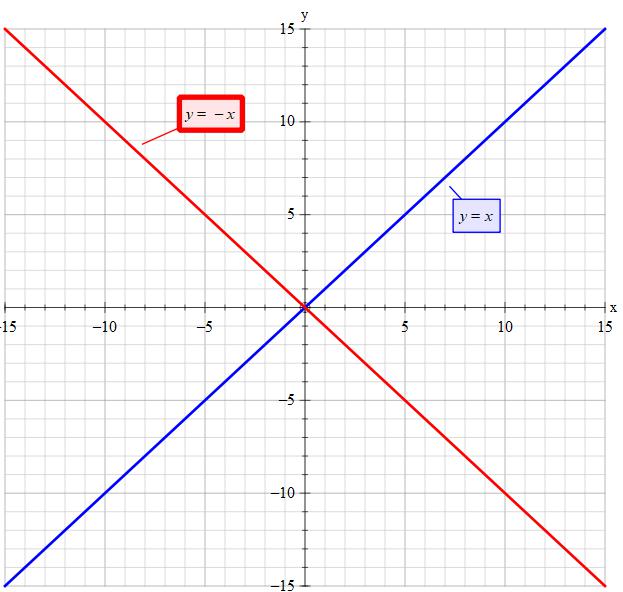
In a 2dimensional Cartesian coordinate system, with x representing the abscissa and y the ordinate, the identity line or line of equality is the y = x line The line, sometimes called the 11 line, has a slope of 1 When the abscissa and ordinate are on the same scale, the identity line forms a 45° angle with the abscissa, and is thus also, informally, called the 45° line Explanation The equation y = − x can be written in slope intercept form as y = − 1 1 x 0 making the y intercept at (0,0) and the slope − 1 1 Begin by graphing the y intercept at the origin (0,0) and then use the slope down 1 for 1 and over 1 to map the remaining points Right, plotting any variable against itself is a line with an intercept at 0 and slope of 1 (x=1*x0) SAS has options to add vertical or horizontal reference lines (x=5 or y=10) but not for x=y That it why you would need to either plot another line (x*x or y*y) or use the annotation facility to draw a line on top of the graph
Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutesThis would be similar to stretching horizontally by multiplying all x coordinates by 5 while leaving the y coordinates unchanged The easiest way is to rotate axes Define a new set of axes by s = x y, t = y − x The s axis is the line y = x and the t axis is the line y = − x We can invert the transformation, finding x = 1 2 ( s − tThe simple way to graph y = x1 is to generate at least two points, put those on your graph paper and draw a straight line through them Here's how you geneate the required points Use your equation, y = x1 and choose an integer for x, say x=2, and substitute this into your equation to find the corresponding value of y y = 2 1 y = 1
Triangle ABC is translated using the rule (x, y) → (x 1, y − 4) to create triangle A′B′C′ If a line segment is drawn from point A to point A′ and from point B to point B′, which statement would best describe the line segments drawn? Here's some code that does scatter plot of a number of different series using matplotlib and then adds the line y=x import numpy as np, matplotlibpyplot as plt, matplotlibcm as cm, pylab nseries = 10 colors = cmrainbow (nplinspace (0, 1, nseries)) all_x = all_y = for i in range (nseries) x = nprandomrandom (12)i/100 y = nprandomrandom (12)i/50 pltscatter (x, y, color=colors i) all_xextend (x)If b ≠ 0, the equation = is a linear equation in the single variable y for every value of xIt has therefore a unique solution for y, which is given by = This defines a functionThe graph of this function is a line with slope and yintercept The functions whose graph is a line are generally called linear functions in the context of calculusHowever, in linear algebra, a linear function




Graph Using The Y Intercept And Slope



1
Related » Graph » Number Line » Examples » Our online expert tutors can answer this problem Get stepbystep solutions from expert tutors as fast as 1530 minutes"y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis In this formula y = x 2 ⇒ x 2 = y x 2 = y parabola is not defined for positive values of y hence parabola will be below Xaxis opening downwards and passing through (0, 0) x y 2 = 0 is a straight line To find point of intersection of parabola and straight line solve the parabola equation and the straight line equation simultaneously
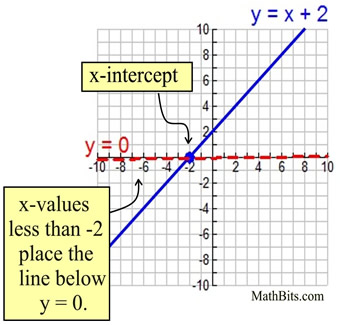



Number Lines And Coordinate Axes Mathbitsnotebook A1 Ccss Math
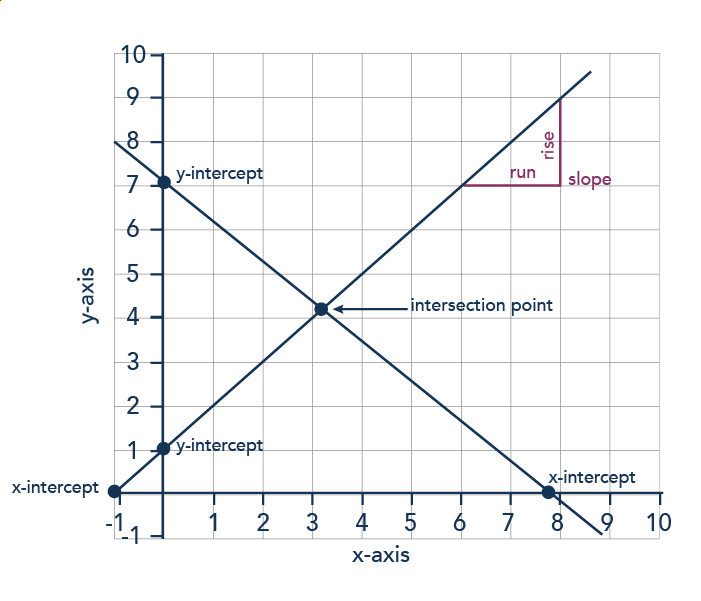



Creating And Interpreting Graphs Microeconomics
Reflection about the line y = x And also, the line x = 2 (line of reflection) is the perpendicular bisector of the segment joining any point to its image Students can keep this idea in mind when they are working with lines of reflections which are neither the xaxis nor the yaxis Apart from the stuff given in this section, if you needCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history Line l, has the equation y = x 4 and line la has the equation y = x – Line l, has the equation y = x 4 and line la has the equation y = x – 4 Find the distance between l, and la Round your answer to the nearest tenth




Graph Using Intercepts
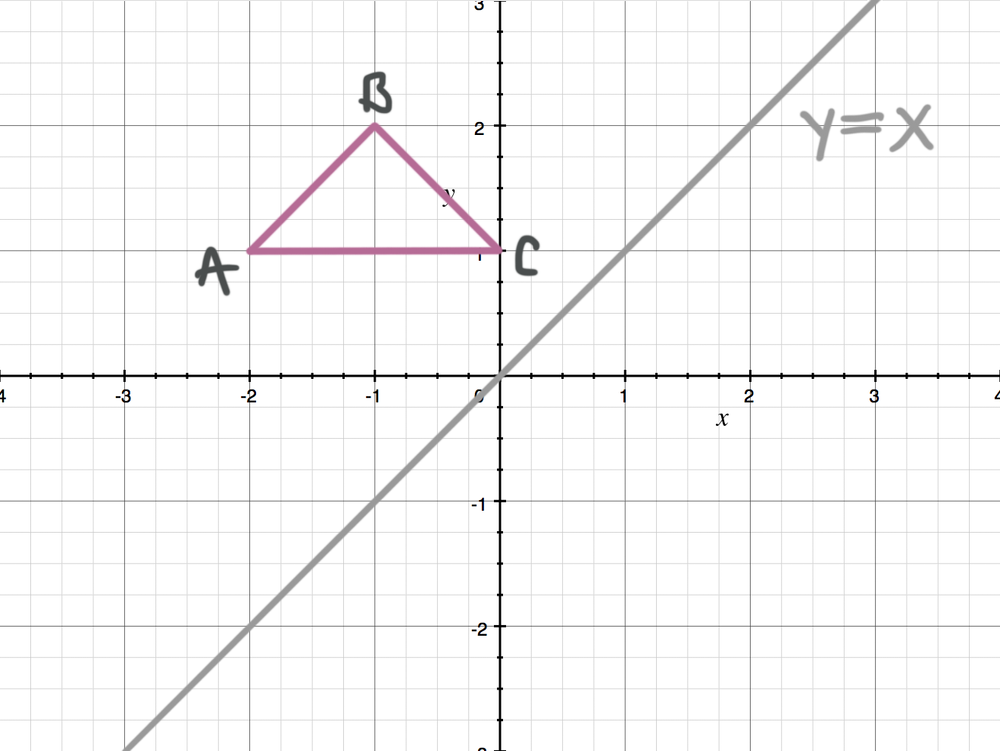



Reflecting Figures In Coordinate Space Krista King Math Online Math Tutor
The line that represents y=x has a slope of 1/1 If i am considering a point, ill refer to it as A at (4,3) and reflect it over line y=x i will be at (4,3) which i will refer to as point B I can prove this relationship using simple geometry I wiSolution Steps y = x2 y = x 2 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side x2=y x 2 = y Subtract 2 from both sides Subtract 2 from both sidesThe line y=x, when graphed on a graphing calculator, would appear as a straight line cutting through the origin with a slope of 1 When reflecting coordinate points of the preimage over the line, the following notation can be used to determine the coordinate points of the image r y=x
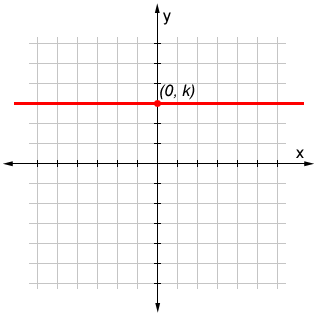



Horizontal Line




Identifying The Intercepts On The Graph Of A Line Prealgebra
Use the function abline (a=0, b=1) where a and b are the intercept and slop of the line respectively This draws you a straight line of the form Y = a b*xEqual to its perpendicular distance from a fixed straight line (called the directrix) (Fig 5) is called a parabola Now, by substituting a Symmetry about the line y = x — Any function f(x,y) = 0 is said to be symmetrical about the line y = x, if there will not be any change in the equation f(x,y) = 0 after interchanging x and y so, Find the equation of image line and reflected line of 2x3y5=0 through the line mirror y=x 50k 1009k 546 Find the equation of the image of the circle in the line mirror 66k 1317k 346 The equation of the line AB is If A and B lie on




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
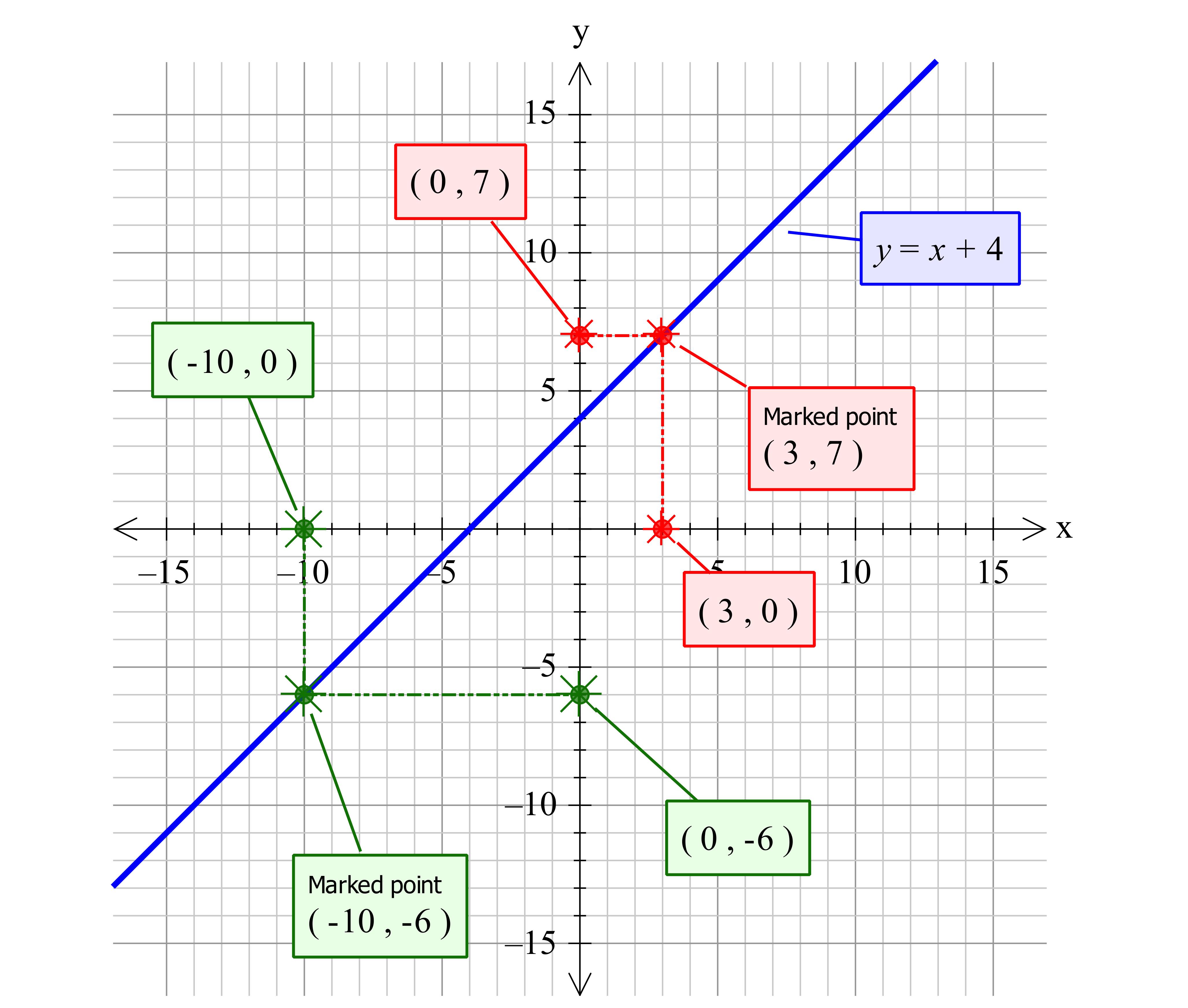



How Do You Graph Y X 4 Socratic
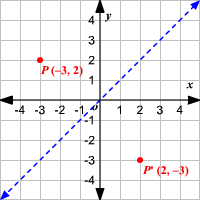
The Lesson A shape can be reflected in the line y = xIf point on a shape is reflected in the line y = x, the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate The image below shows a point on a shape being reflected in the line y = x The point A has Cartesian coordinates (2, 3);The line y = x is the point (y, x) Reflect over any line Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure The line of reflection will lie directly in the middle between the original figure and its image# Add a vertical line segment sp geom_segment(aes(x = 4, y = 15, xend = 4, yend = 27)) # Add horizontal line segment sp geom_segment(aes(x = 2, y = 15, xend = 3, yend = 15)) Note that, you can add an arrow at the end of the segment grid package is required




Reflecting A Shape In Y X Using Cartesian Coordinates Key Stage 3




How To Find A Reflection Image
Reference lines horizontal, vertical, and diagonal Source R/geomabliner, R/geomhliner, R/geomvliner geom_ablineRd These geoms add reference lines (sometimes called rules) to a plot, either horizontal, vertical, or diagonal (specified by slope and intercept) These are useful for annotating plotsAnswer to Find the area of the region in the first quadrant bounded by the line y = x, the line x = 2, the curve y = 1/x^2, and the xaxis By If P is a point on the parabola y = x2 4 which is closest to the straight line y = 4x – 1, then the coordinates of P are (1) (3, 13) (2) (1, 5) (3) (–2, 8) (4) (2, 8) jee jee main jee main 21 Please log in or register to add a comment




Slope Wikipedia




Reflect Shape A In The Line Y X Brainly Com
For example, when point P with coordinates (5,4) is reflecting across the Y axis and mapped onto point P', the coordinates of P' are (5,4)Notice that the ycoordinate for both points did not change, but the value of the xcoordinate changed from 5 to 5 You can think of reflections as a flip over a designated line of reflection Here is the line integral for this curve ∫ C 2 x d s = ∫ 1 − 1 t √ 1 0 d t = 1 2 t 2 1 − 1 = 0 Note that this time, unlike the line integral we worked with in Examples 2, 3, and 4 we got the same value for the integral despite the fact that the path is different This will happen on occasion How to graph this equation Step 1 Draw up a table of values that can be used to construct the graph Step 2 Draw your yaxis as a vertical line and your xaxis as a horizontal line Mark the relevant points for the x and y values Draw freehand as best as you can a smooth curve that passes through those points Answer link




Reflection




How To Reflect A Graph Through The X Axis Y Axis Or Origin
Equation of a Straight Line The equation of a straight line is usually written this way y = mx b (or "y = mx c" in the UK see below) What does it stand for? Example 3 Find the area of the region bounded by the curve 𝑦=𝑥2 and the line 𝑦=4 Given that y = 4 Let Line AB represent y = 4 Also, y = x2 x2 = y Let AOB represent x2 = y We have to find area of AOBA Area of AOBA = 2 × Area BONB = 2 04𝑥 𝑑𝑦 We know that 𝑥2= 𝑦Pick a number for x, say 0 then y=0 now pick x=1 then y=1 now you have two points (0,0) and (1,1) (you only need two points to graph a line so plot those points, connect them and




Reflections Across Y X Geogebra




Reflections Through The Axes And The Lines Y X And Y X Geogebra
"y=mxb" is the formula of a straight line drawn on Cartesian coordinate system in which "y" is the vertical axis and "x" the horizontal axis In this formula When reflecting over the line y=x, we switch our x and y, and make both negative Reflection Over Y = X In order to define or describe a reflection, you need the equation of the line of reflection The four most common reflections areThe point located (3,1) is reflected across the yaxisWhat are the coordinates of the reflected p The point A (7,5) is reflected over the line x=5 and then is reflected over the line x=2 what are The point A (3, 4) is reflected over the line x = 2, and then is reflected over the line x= 4




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
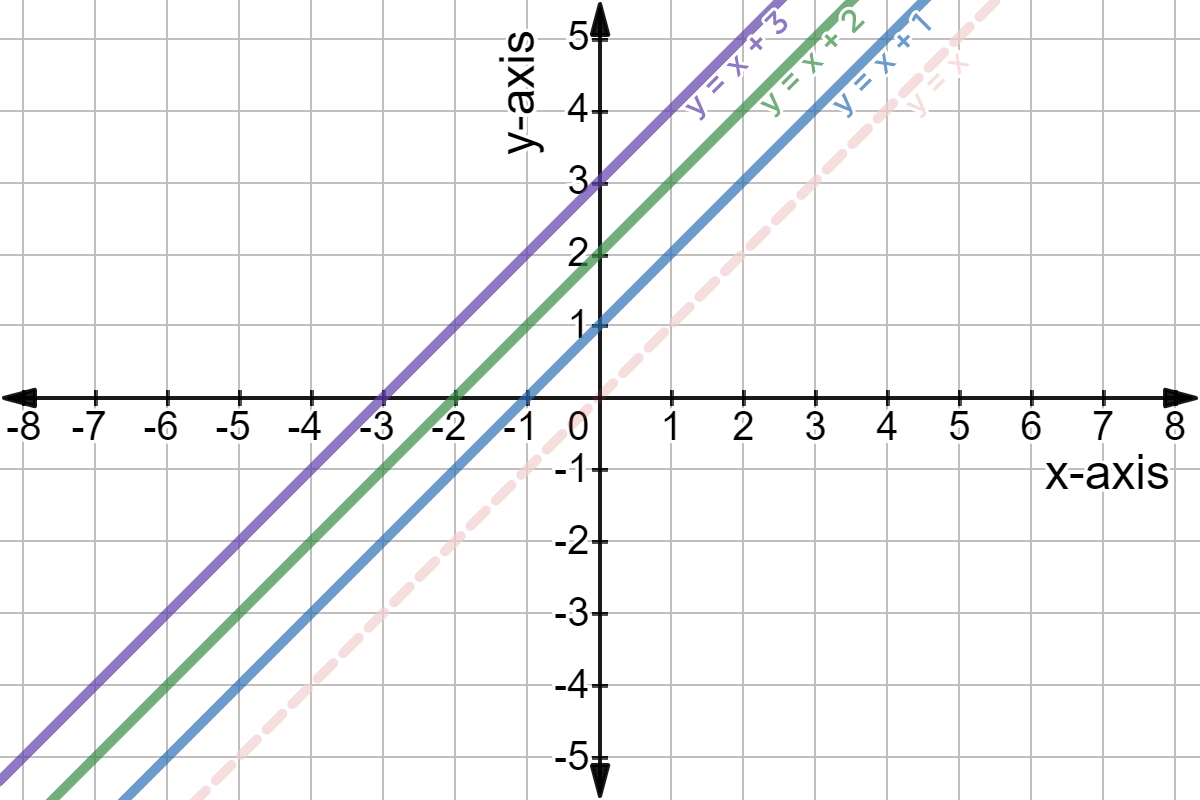



Graphing Linear Functions Expii
The Lesson A shape can be reflected in the line y = −x If point on a shape is reflected in the line y = −x both coordinates change sign (the coordinate becomes negative if it is positive and vice versa) the xcoordinate becomes the ycoordinate and the ycoordinate becomes the xcoordinate The image below shows a point on a shape being reflected in the line y = −xThe reflected point A' has Cartesian coordinates (3, 2) 1 Answer1 Active Oldest Votes 2 The terms diagonal and antidiagonal are descriptive and "culturally apt" The first is standard in geometry and topology (the diagonal embedding of a topological space X is the inclusion X ↪ X × X defined by x ↦ ( x, x) ), and I'm almost positive I've seen the second in connection with the normal bundle
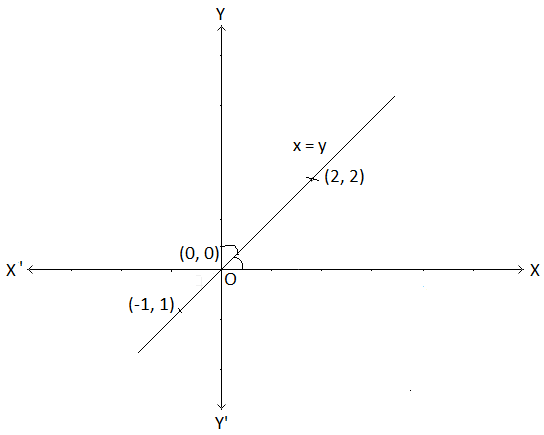



Graph Of Standard Linear Relations Between X Y Graph Of Y X
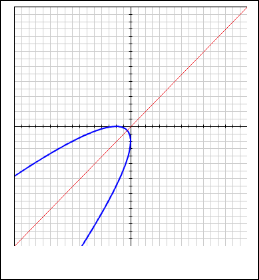



A Parabola Symmetrical To Y X Line
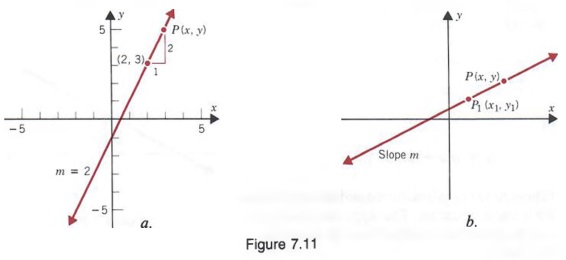
Slope or Gradient y when x=0 (see Y Intercept) y = how far up x = how far along m = Slope or Gradient (how steep the line is)



Search Q Reflection Over Y 3d X Tbm Isch



Assignment 2 Write Up



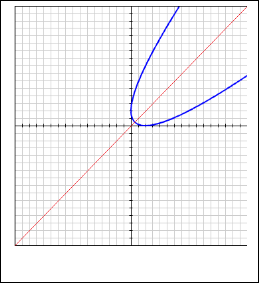
Graph Of Standard Linear Relations Between X Y Graph Of Y X



A Parabola Symmetrical To Y X Line
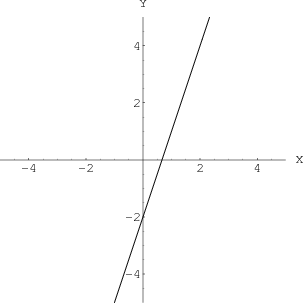



A Line Or A Plane Or A Point Math Insight



How Do You Graph The Line Y X 2 Example




Ixl Graph A Line From An Equation In Slope Intercept Form 8th Grade Math




Unit 5 Section 2 Straight Line Graphs



Mathscene Vectors Lesson 5




Reflection Over The Line Y X Math Showme
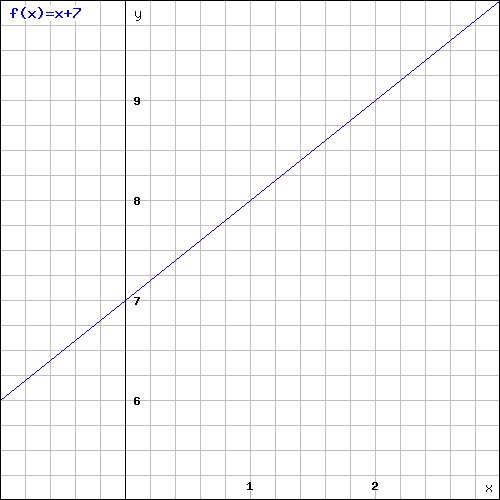



Functions And Linear Equations Algebra 2 How To Graph Functions And Linear Equations Mathplanet




Reflection Transformation Matrix
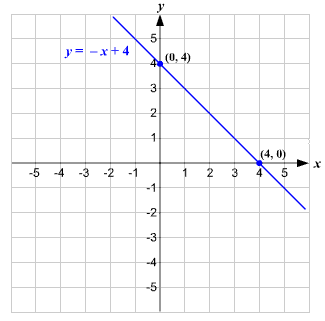



Solve System Of Linear Equations Graphically



Operations On Functions Reflections And Rotations Sparknotes




Learn About Reflection Over The Line Y X Caddell Prep Online
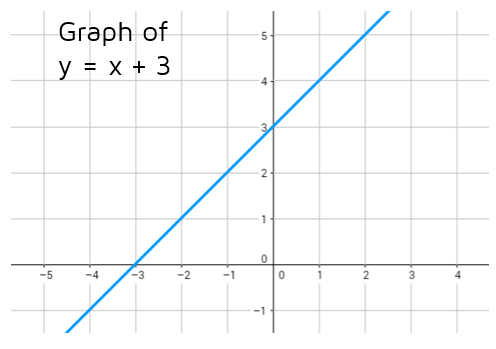



Graphing Linear Inequalities Kate S Math Lessons




Transformations Of Graphs




Intercepts Of Lines Review X Intercepts And Y Intercepts Article Khan Academy



Reflections




Draw The Graph Of Linear Equations Y X And Y X On The Same Certesian Plane What Do You Observed Brainly In



Graph Of Standard Linear Relations Between X Y Graph Of Y X



Inequalities Graphing Inequalities Sparknotes




Reflection Mathbitsnotebook A1 Ccss Math



What Does It Mean To Reflect Over The Y X Line Quora



Horizontal And Vertical Lines




Rules For Reflections Read Geometry Ck 12 Foundation



Graph Graph Equations With Step By Step Math Problem Solver




Reflection In The Line Y X Geogebra



How To Draw The Graph Of Y X And Y X In The Same Graph Quora



What Is The Basic Difference Between The Lines Y X And Y X Socratic



Graphing Linear Inequalities
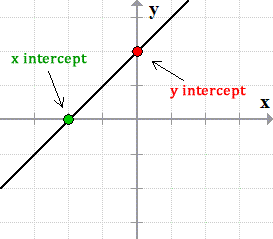



Graph A Line Using X And Y Intercepts Chilimath



Slope Fields
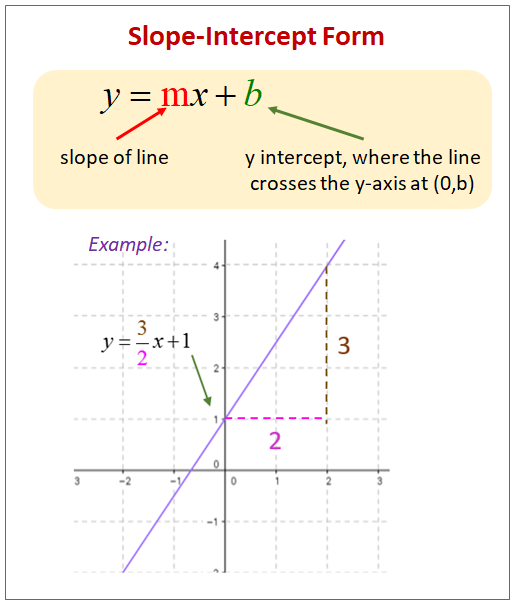



Equation Of A Line Video Lessons Examples Solutions
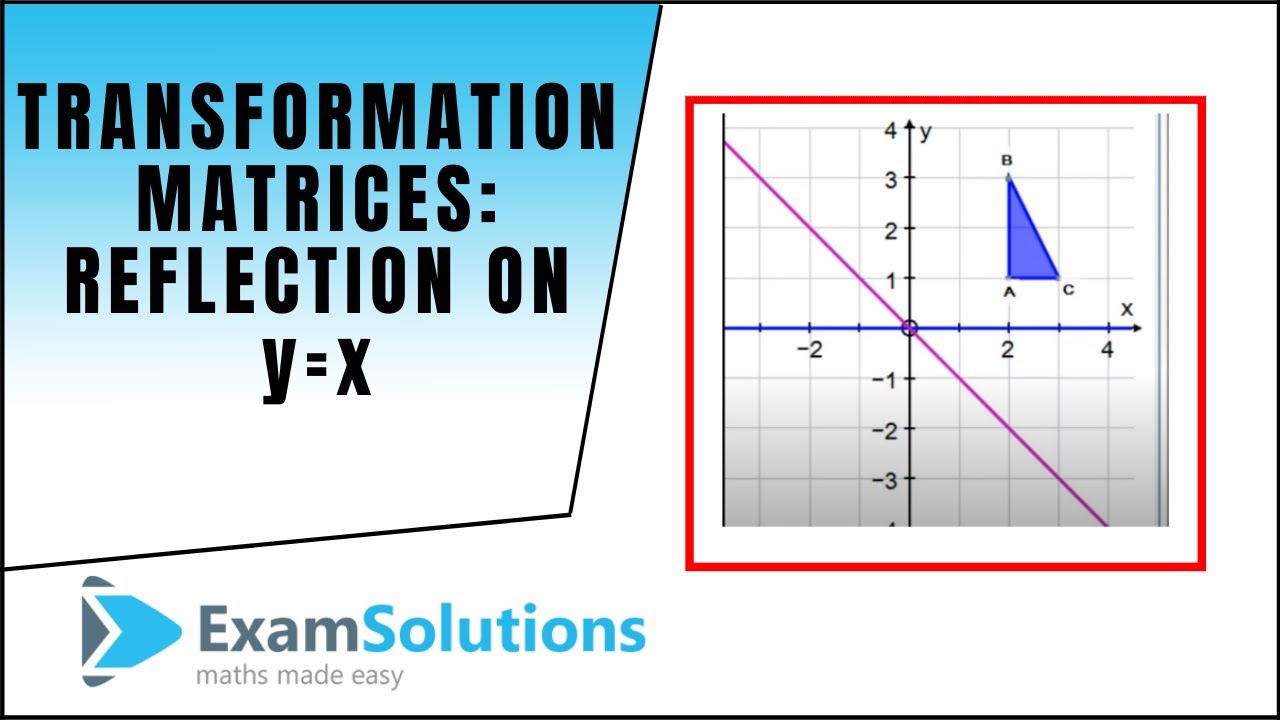



Transformation Matrices Reflection The Line Y X Examsolutions Maths Tutorials Youtube



1




Reflection Over The X And Y Axis The Complete Guide Mashup Math
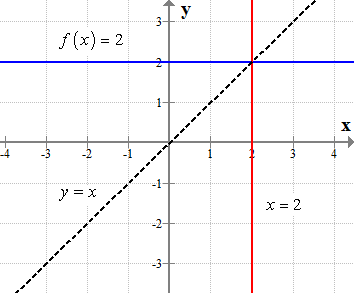



Inverse Of Constant Function Chilimath
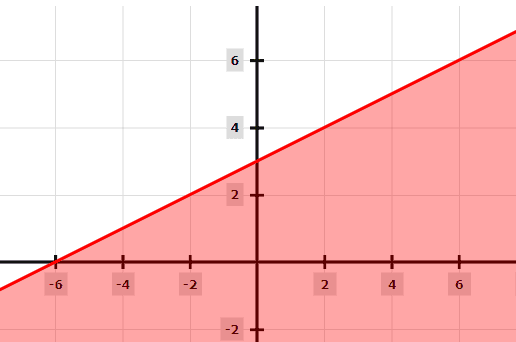



Graphing Linear Inequalities Explanation Examples




Reflecting Functions Examples Video Khan Academy




Reflection Transformation Matrix




Below Is The Graph Of Y X 3 Translate It To Make Chegg Com



Solution Graph The Line With Equation Y X 5



Math Alive Geometry 1



How To Graph The Inverse Of A Function Dummies



Math Alive Geometry 1
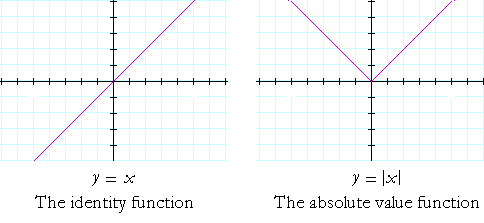



Graph Of A Parabola Topics In Precalculus




Common Reflections Key Stage 3




Distance Between Parallel Lines Read Geometry Ck 12 Foundation
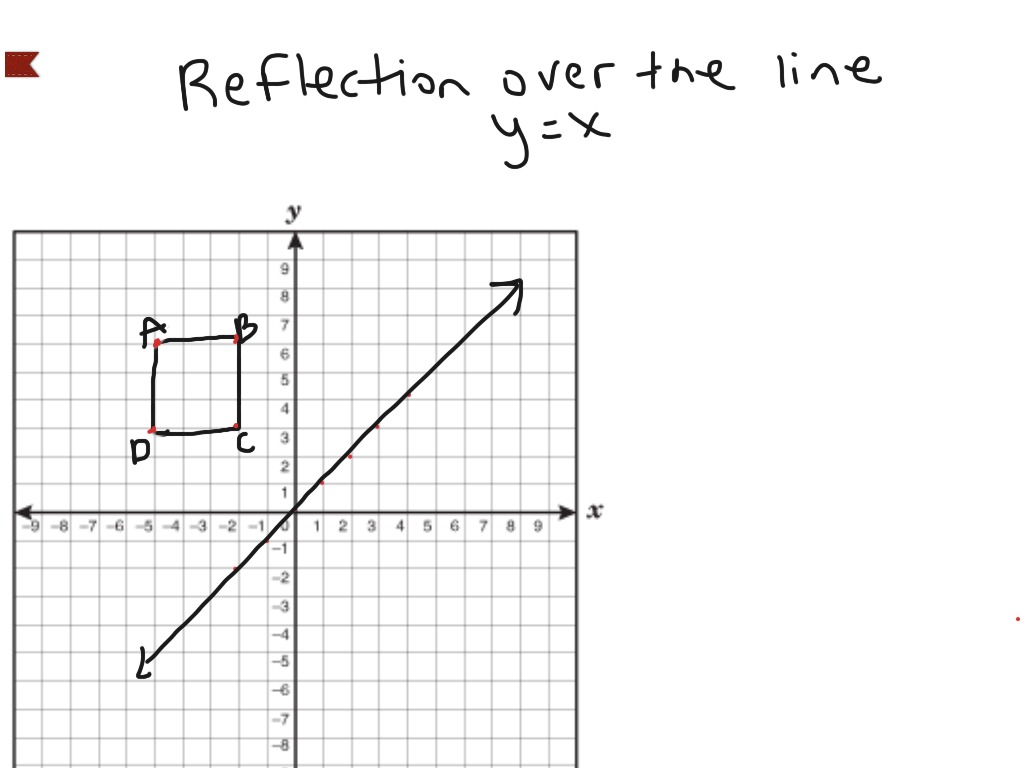



Reflection Over The Line Y X Math Showme



Reflection Rules



Ch 3 4
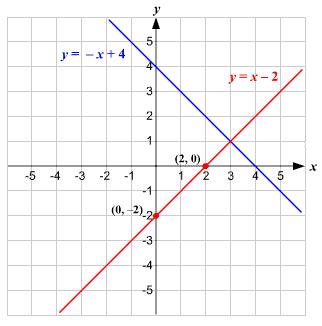



Solve System Of Linear Equations Graphically
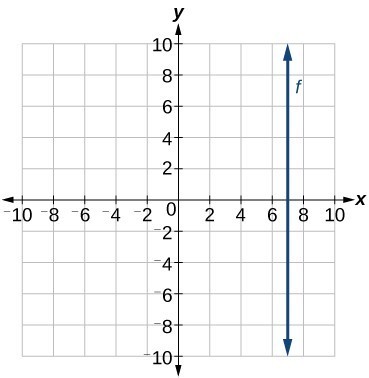



Write The Equation For A Linear Function From The Graph Of A Line College Algebra
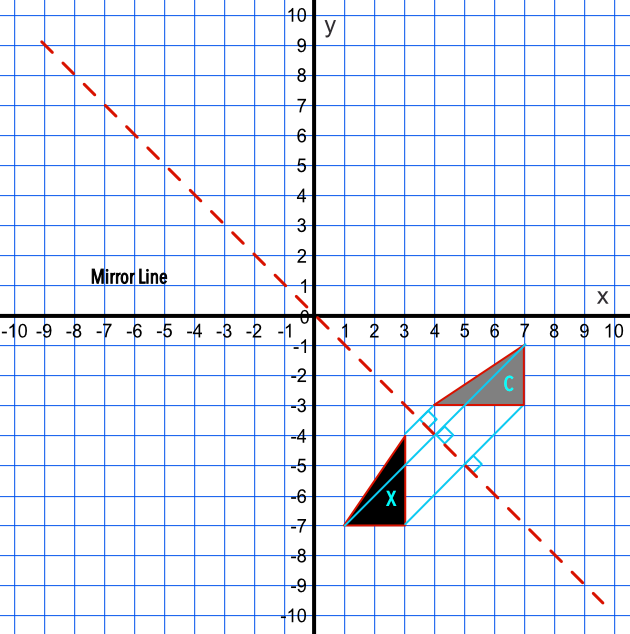



Reflection



Solution How To Draw The Line Y X On Graph
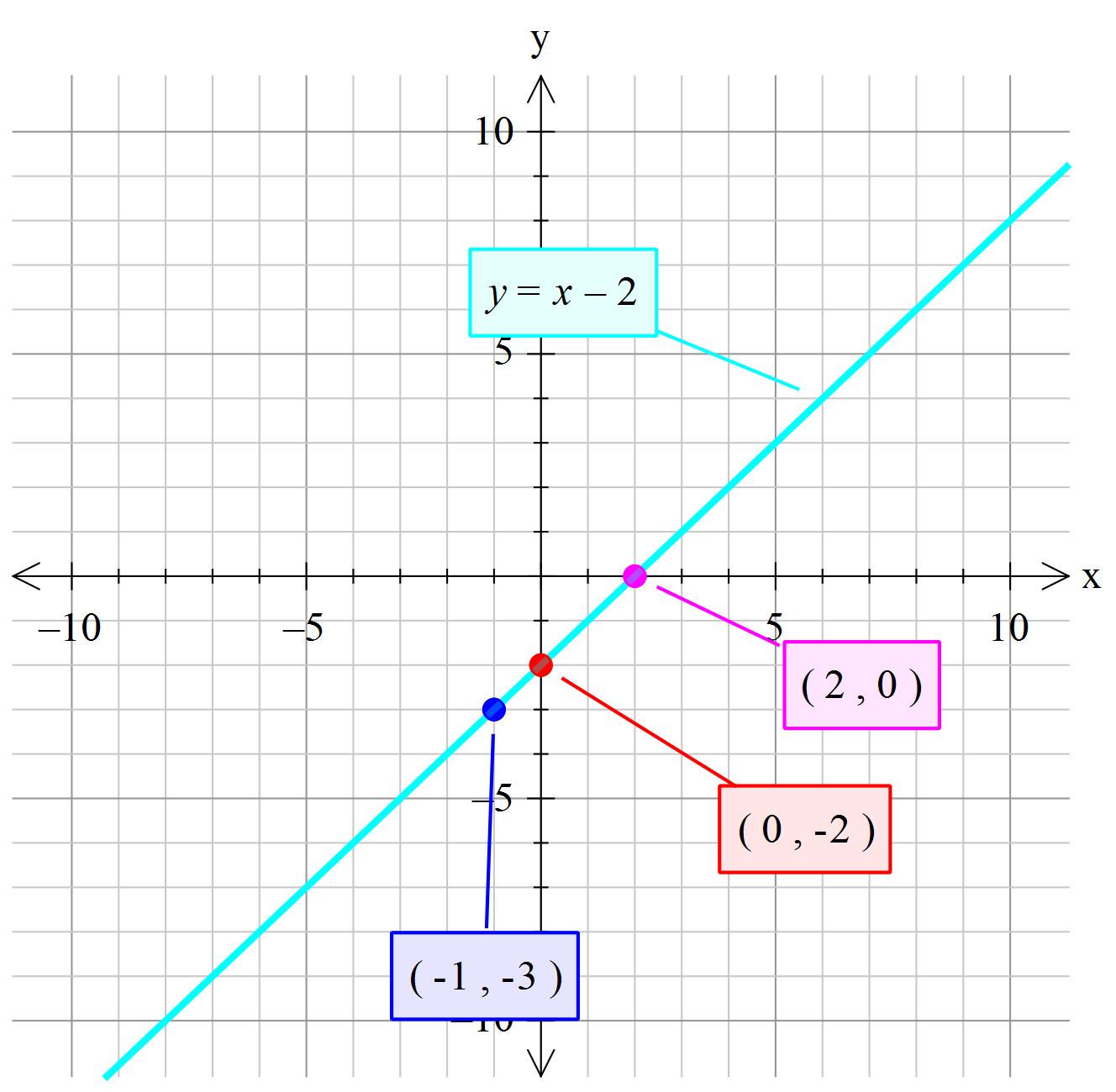



How Do You Graph The Line X Y 2 Socratic
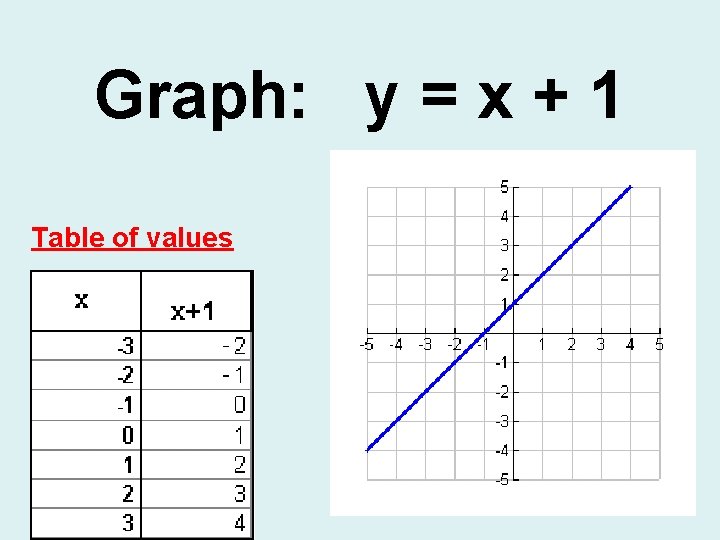



Graph The Linear Equation Yx 2 1 Draw




Slope Intercept Form Graphing Lines Free Math Help



Graphing Systems Of Inequalities
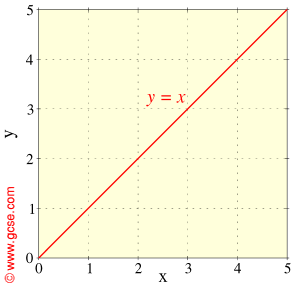



Gcse Maths Plotting X Y Graphs
/1000px-Parabola_features-58fc9dfd5f9b581d595b886e.png)



How To Find Quadratic Line Of Symmetry




Equation Xy Yx Wikipedia



Solution How Do You Graph Y X 1



Reflection Over The X And Y Axis The Complete Guide Mashup Math




Transformation Reflection Over The Line Y X Youtube



Linear Equations In The Coordinate Plane Algebra 1 Visualizing Linear Functions Mathplanet




Reflection Over The Y X Line Youtube




Adding Y X To A Matplotlib Scatter Plot If I Haven T Kept Track Of All The Data Points That Went In Stack Overflow




How To Find A Reflection Image
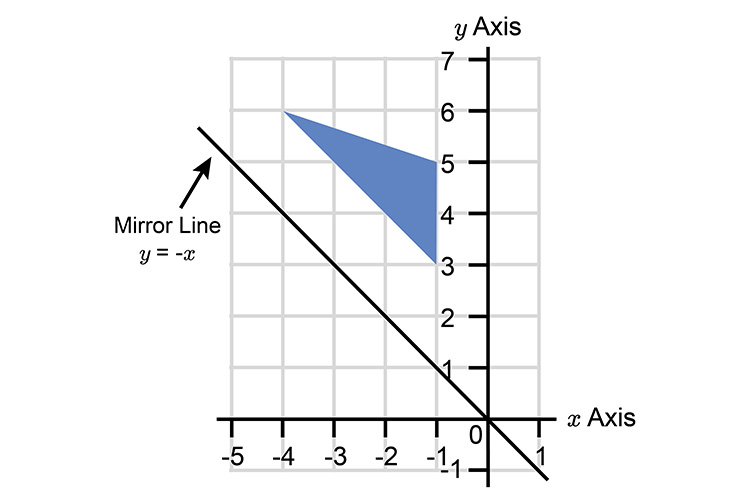



Mirror Lines Can Be Placed Anywhere You Just Reflect




How To Reflect A Graph Through The X Axis Y Axis Or Origin



How Do You Graph The Line Y X 2 Example
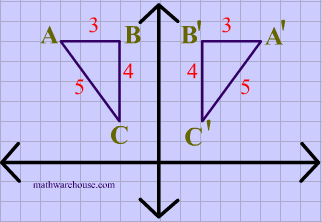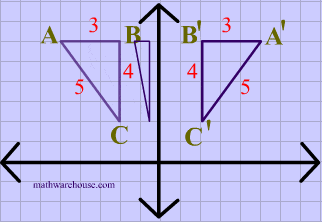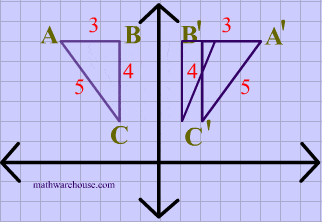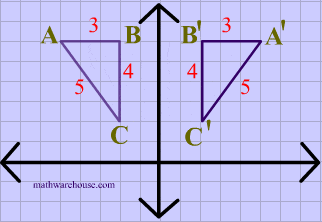



Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines




File Y X 2 Svg Wikimedia Commons



Function And Relation Library



Equation Of A Horizontal Or Vertical Line Expii



Content The Concept Of A Function
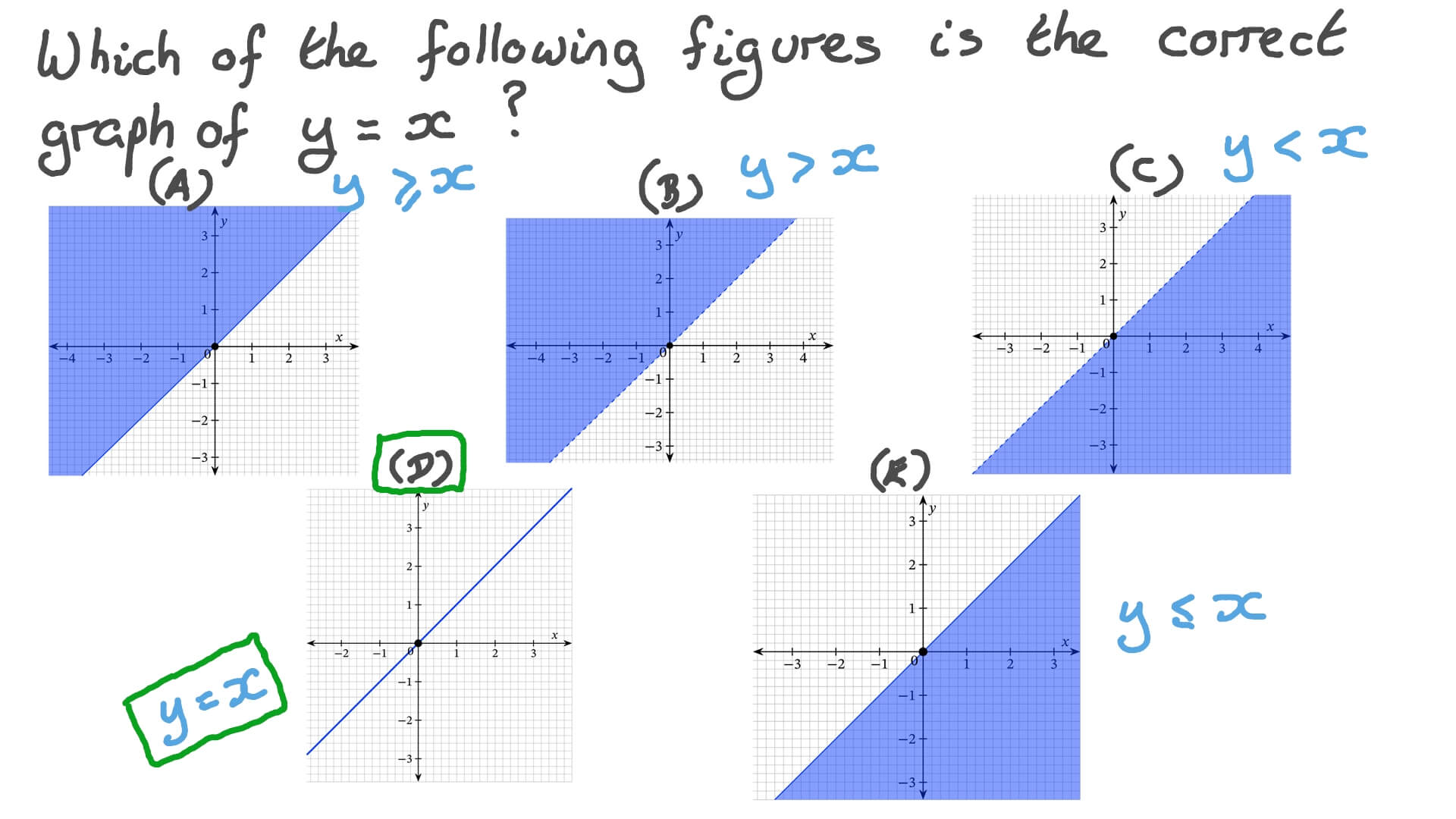



Question Video Graphs Of Linear Inequalities Nagwa




Draw Graph Of The Equation Y X 5



Graph Graph Equations With Step By Step Math Problem Solver




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com



0 件のコメント:
コメントを投稿